题解 P2757 【[国家集训队]等差子序列】&& CF452F Permutation

发表于 | 更新于

$Description$

给你一个$1$到$n$的排列，你需要判断该排列内部是否存在一个$3$个元素的子序列(可以不连续)，使得这个子序列是等差序列。

$Solution$

思路一$:bitset$优化暴力

枚举中间的数$,$判断一下这个数的对称的两侧$,$如果一侧的数出现了但是另一侧的没出现。那么一定存在一个可行方案

思路二$:$线段树维护$hash$值

从左到右，设当前数$w_j$为中间那一个,那么有以下两种情况

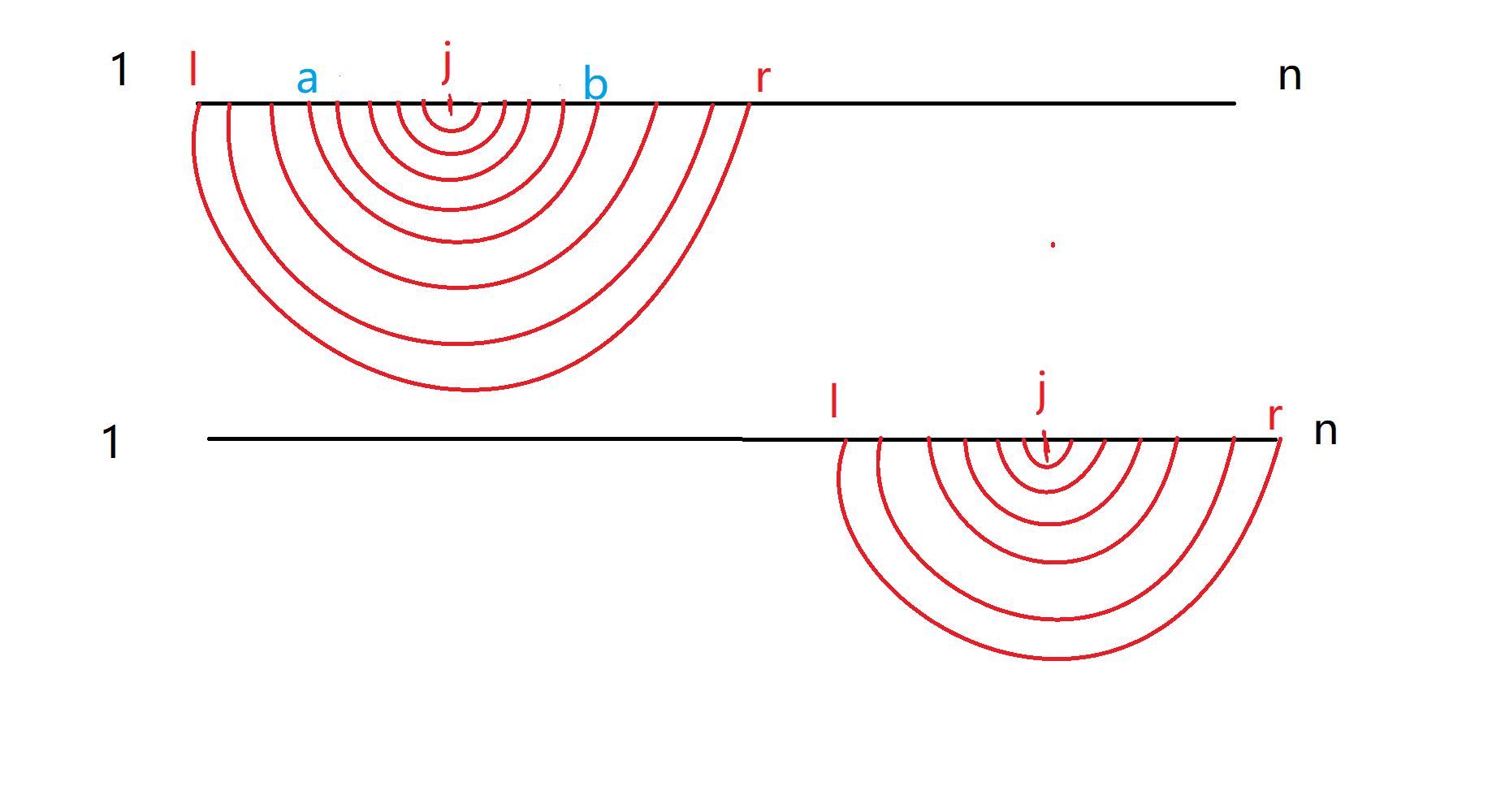
显然对于$l\sim j$与$r\sim j$如果有一位不相等（也就是它们的值不相等）那么就成立，因为一个在前面出现过了，另一个在后面还没出现过。

如上图中我们假设$c_a,c_b$不相等$($设$c_a=1,c_b=0)$,那么$a$在$w_j$之前就出现过$($即原序列中在$w_j$前$),$而$b$在$w_j$之后出现$($即原序列中在$w_j$后$)$。

$Code$

$bitset$优化暴力

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <bits/stdc++.h>
#define ll long long
#define inf 0x3f3f3f3f
#define re register
#define N 560000
using namespace std;

inline int read(){
    int x=0,w=0;char ch=getchar();
    while (!isdigit(ch))w|=ch=='-',ch=getchar();
    while (isdigit(ch))x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
    return w?-x:x;
}
int n,a[N];
bool check(){
    bitset<10060>b,c;b.reset();
    for (int i=1;i<=n;++i)c.set(i);
    for (int i=1;i<=n;++i){
        b.set(a[i]);c.reset(n-a[i]+1);
        if (((b>>(a[i]+1))&(c>>(n-a[i]+1+1))).any()){
            return 1;
        }
    }
    return 0;
}
signed main(){
    int T=read();
    while (T--){
        n=read();
        for (int i=1;i<=n;++i)a[i]=read();
        if (check()){puts("Y");continue;}
        reverse(a+1,a+1+n);
        if (check())puts("Y");
        else puts("N");
    }
    return 0;
}

线段树维护$hash$值

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include <bits/stdc++.h>
#define int long long
#define inf 0x3f3f3f3f
#define re register
#define N 1200000
#define base 131
#define mod 998244353
#define ls(k) (k<<1)
#define rs(k) (k<<1|1)
#define pushup(k) a[k]=a[ls(k)]+a[rs(k)],b[k]=b[rs(k)]+b[ls(k)]
using namespace std;
int po[N];
struct node{
    int val,len;
    inline void init(){val=0,len=0;};
    friend node operator +(node a,node b){
        return (node){(a.val*po[b.len]%mod+b.val)%mod,a.len+b.len};
    }
}a[N],b[N];
inline int read(){
    int x=0,w=0;char ch=getchar();
    while (!isdigit(ch))w|=ch=='-',ch=getchar();
    while (isdigit(ch))x=(x<<1)+(x<<3)+ch-'0',ch=getchar();
    return w?-x:x;
}
void build(int k,int l,int r){
    if (l==r){
        a[k]=b[k]=(node){0,1};
        return;
    }
    int mid=(l+r)>>1;
    build(ls(k),l,mid);
    build(rs(k),mid+1,r);
    pushup(k);
}
void change(int k,int l,int r,int x){
    if (l==r){
        a[k]=b[k]=(node){1,1};
        return;
    }
    int mid=(l+r)>>1;
    if (x<=mid)change(ls(k),l,mid,x);
    else change(rs(k),mid+1,r,x);
    pushup(k);
}
node query1(int k,int l,int r,int x,int y){
    if (x<=l&&r<=y)
        return a[k];
    int mid=(l+r)>>1;node res;res.init();
    if (x<=mid)res=res+query1(ls(k),l,mid,x,y);
    if (mid<y) res=res+query1(rs(k),mid+1,r,x,y);
    return res;
}
node query2(int k,int l,int r,int x,int y){
    if (x<=l&&r<=y)
        return b[k];
    int mid=(l+r)>>1;node res;res.init();
    if (mid<y) res=res+query2(rs(k),mid+1,r,x,y);
    if (x<=mid)res=res+query2(ls(k),l,mid,x,y);
    return res;
}
signed main(){
    po[0]=1;
    int n=read(),flag=0;
    for (int i=1;i<=n;++i)po[i]=po[i-1]*base%mod;
    build(1,1,n);
    for (int i=1;i<=n;++i){
        int x=read();
        if (flag)continue;
        change(1,1,n,x);
        int len=min(x-1,n-x);
        if (len<=0)continue;
        if (query1(1,1,n,x-len,x-1).val!=query2(1,1,n,x+1,x+len).val){flag=1;continue;}
    }
    puts(flag?"YES":"NO");
    return 0;
}